Update: 08/12/2022

Sporo osób pyta co to właściwie ten Bayes, średnia bayesa, bajesjańska, bajesowska, bayesa… no to na szybko. Primo: to jest Bayes. Thomas Bayes:

Ów Thomas Bayes, XVIII wieczny matematyk angielski (i jak widać na rycinie: duchowny) sformułował twierdzenie (praca w tym temacie – “Essay Towards Solving a Problem in the Doctrine of Chances” – została opublikowana pośmiertnie) dzisiaj nazywane, a jakże, Twierdzeniem Bayesa.

Opisuje ono prawdopodobieństwo zdarzenia na podstawie wcześniejszej wiedzy o warunkach, które mogą być związane ze zdarzeniem. Na ten przykład: jeśli bierzemy losowe piwo i je pijemy, to prawdopodobieństwo jakie dobre ono będzie to jakieśtam rozkłady normalne itp. Ale jeśli zastosujemy logikę Bayesa, to sprawdzimy na UT, że ludziom ono nie smakowało zazwyczaj, więc szansa że jest kiepskie jest większa, niż że jest niekiepskie. Ba, jeśli za kiepskie uznały je dwie osoby, to modyfikacja szansy nie jest kolosalna, ale jeśli 200 osób, to już i owszem… Co więcej, nasza ocena jako 201 osoby wpłynie na prawdopodobieństwo kiepskości szacowane dla następnych osób. Brzmi logicznie, nieprawdaż?

Albo od drugiej strony: widzimy na UT, że piwo A ma średnią (arytmetyczną) ocenę 4.5 i 10 wystawionych ocen, zaś piwo B ma 4.4 ale 1000 ocen… i większość osób odbierze takie informacje intuicyjnie tak, że szansa, że piwo B jest zajebiste jest większa niż szansa na zajebistość A.

Acz matematycznie wygląda to koszmarnie, że aż przekleję obrazek z wiki (który u 95% osób, łącznie ze mną, budzi “yyyy, łot?” z usta):

Jak to właściwie przełożyć na piwo? No cóż, to już było przekładane na różne rankingi, najpopularniejszym jaki znam, to top listy z IMDB (tworzone na podstawie ocen użytkowników, i to wyobraźcie sobie, użytkowników bez uprawnień z filmowego odpowiednika PSPD czy BJCP). W świecie piwnym średnia Bayesa (bayesowska, bayesjańska, bajesowska, bajesjańska, bajesa – z wszystkimi formami można się spotkać) jest stosowana przez UT. Konkretnie Top50 piw jest wyliczane na jej podstawie. Analogicznie – była używana przez ś.p. Brewer Stage (i miała priorytet przed również podawaną średnią arytmetyczną, w sensie rankingi były tworzone na podstawie Bayesa a nie arytmetycznej)

Żeby więc przedstawić to już na konkretnym wzorku:

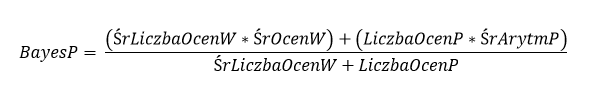
Gdzie:

  • BayesP – Średnia Bayesa danego piwa
  • ŚrLiczbaOcenW – Średnia liczba ocen piwa w całym analizowanym zbiorze
  • ŚrOcenW – Średnia ocen wszystkich piw z całego analizowanego zbioru
  • LiczbaOcenP – Liczba Ocen danego piwa
  • ŚrArytmP – Średnia arytmetyczna danego piwa

Padające w powyższym opisie “cały analizowany zbiór” to rzeczjasna sprawa zależna, od danych statsów, w których Bayes jest wykorzystywany. Może to być komplet czekinów z knajpy, komplet czekinów osoby, komplet czekinów wszystkicj PL festiwali… w podawanych dotąd przykładach: dla UT jest to komplet wszystkich czekinów na UT, dla Brewer Stage jest to komplet czekinów na danym festiwalu.

No to matematycznie chyba już wszystko jasne. Teraz łopatologicznie vel przez machanie rękami. Bo w praktyce działa to tak:

Każda kolejna ocena danego piwa popycha jego średnią Bayesa w stronę jego średniej arytmetycznej wbrew przyciąganiu, którego środek jest tam, gdzie średnia arytmetyczna całego analizowanego zbioru. Dość logiczne i obrazowe – przynajmniej dla mnie. Ale w związku z faktem, że jestem wzrokowcem, pozwolę sobie na graficzne przykłady

“Cały analizowany zbiór” w tym przykładzie to komplet czekinków na PL festiwalach w 2022 roku. Sporo było kilka dni temu statystyk dla tego zbioru, no to niech się jeszcze raz przyda – w sumie przykład dość fajny, bo życiowy, W tym zbiorze możemy na start policzyć wskaźniki:

  • ŚrLiczbaOcenW (Średnia liczba ocen piwa w całym analizowanym zbiorze) – prosto: 47707 ocen jakiegokolwiek piwa podzielone przez 4442 różne piwa daje nam średnią w przybliżeniu 10.74
  • Średnia ocen wszystkich piw z całego analizowanego zbioru – kilka kliknięć w excelku i wychodzi koło 3.819

I teraz dwa wykresiki, przedstawiające najpierw średnią arytmetyczną każdego z piw na osi liczby czekinów, zaś następnie średnią bayesa na tej samej osi.




Chyba ładnie widać, jak te kropki są "dociskane" do linii średniej całego zbioru (zaznaczonej na czerwono), przy czym tym silniej dociskane, im mniejsza liczba ocen. Zresztą można sobie popatrzeć na konkretne przykłady, wartości liczbowe dla jakichś charakterystycznych kropek.

Dodatkowo dzięki Bayesowi wychodzi na to, że rozrzut ocen dla danych piw jest pi razy drzwi podobny, niezależnie od liczby ocen. Przy średniej arytmetycznej ten rozrzut jest tym większy, im mniej ocen.

Jeśli zaś powyższe dwa wykresy przedstawić na jednym obrazku, tyle, że na osiach średnie - bayesa i arytmetyczną, zaś liczbę ocen obrazować jako wielkość kropki, wychodzi dla tej próbki danych coś takiego:

Widać, jak punkty dla kolejnych liczb ocen układają się w linie z jednym punktem wspólnym o współrzędnych na obu osiach równych średniej ocenie całego zbioru. Z kolei linie te są obracane względem tego wspólnego punktu, dążąc wraz ze wzrostem liczby ocen do (zaznaczonej na wykresie na czerwono) linii, gdy średnia arytmetyczna równa się średniej Bayesa. Elegancka ta matematyka, nawet na poziomie podstawówki

Dodatkowy przykład - tym razem czysto teoretyczny - pokaże na wykresie, jak kolejne oceny wpływają na średnią Bayesa. Teoretyczny, bo obrazuje sytuację absolutnie nieżyciową czy wręcz utopijną, gdy to oceniający na UT w trakcie festiwali w PL w 2022 (czyli opieramy się o dane z poprzednich przykładów, w szczególności o średnią całości) są bardzo zgodni, i klikając kolejne oceny piw, wszyscy klikają te same, odpowiednio:

  • jakiś lambik z PL, wyjątkowo udany i hajpowany, ocena 4,75
  • jakaś ipka, umiarkowanie udana, ocena 3,5
  • jakiś red lager, zupełnie nieudany, ocena 2,0

i tak to będzie się kształtowało jeśli idzie o Bayesa na przestrzeni kolejnych (od 1 do 100) czekinów:

Szary obszar na powyższym wykresie jest ostatnim aspektem wszelakich tabelek czy rankingów opartych na średniej Bayesa. A zarazem z rzeczoną średnią nie mający nic wspólnego.

Chodzi o to, że nawet w średniej Bayesa niska liczba ocen zmniejsza wiarygodność oceny. Dlatego też zarówno IMDB, jak i UT oraz BS założyły minimalną liczbę ocen, która jest konieczna by być w jakimśtam rankingu uwzględnianym.

Dla UT i ich list Top50 piw jest to arbitralnie założone minimum 150 ocen. Dla Brewer Stage jest na to kolejny, acz banalny wzorek: Minimalna Liczba ocen piwa by piwo było prezentowane w zestawieniach czy rankingach = 0.15% liczby wszystkich ocen w całym analizowanym zbiorze. Przy czym minimum 3 i maksimum 15. Dla browaru zaś owa minimalna liczba = 3 * minimalna liczba wyliczona dla piwa. Zresztą tego wzorku staram się przestrzegać we własnych piwnych statystykach, acz pojęcia nie mam, skąd się owo akurat piętnaście setnych procenta wzięło właściwie...

I powyższe pitu pitu chyba zamyka temat :> Więc tylko kilka linków:

PS: aha, wbrew tej ścianie tekstu czasem trzeba w warunkach polowych, w knajpie cycuś i to po kilku czekinkach odpowiedzieć na "Co to jest ten Bayes?". Wtedy w krótkich, żołnierskich słowach mówię: "no to taka średnia ocena, tylko że uwzględnia popularność". I właściwie nawet nie kłamię.